|
Rigidità dei solai e dei tetti
|
Quando i solai possono essere considerati rigidi e quando invece noDi solito i solai in c.a. vengono modellati come diaframmi rigidi, mentre la copertura in legno (tradizionale) viene considerata non rigida.I criteri di rigidità fanno riferimento alle EC8 §4.3.1 e prassi NTC 2018.Un impalcato può essere assunto infinitamente rigido in pianta se le sue deformazioni nel proprio piano sono piccole rispetto alle derivazioni laterali dei telai/setti del piano (regola pratica: ≤ ~10% dello drift di piano).Cosa si intende per drift di piano:Il drift di piano (o interstorey drift) è la deformazione laterale relativa tra due piani consecutivi durante l’azione sismica.Spostamento relativo: Δ=∣ upiano sup−upiano inf∣Rapporto di drift (adimensionale): θ=Δ/h h è l’altezza interpiano.Esempio: se h=3.00 m e lo spostamento relativo è Δ=6 mm, allora θ=0,006/3=0,002=0,20%A cosa serve:misura la domanda di deformazione sui telai/setti;governa il danno agli elementi non strutturali (tamponamenti, tramezzi);entra nei controlli di instabilità P–Δ.Cosa si intende per infinitamente rigido in pianta:“Infinitamente rigido in pianta” (per un impalcato) significa che, sotto azioni orizzontali, il solaio si deforma trascurabilmente nel suo piano rispetto allo spostamento laterale dei telai/setti del piano. In pratica il diaframma “si muove come un corpo rigido”: mantiene allineati i nodi, ripartisce le forze ai sistemi verticali in base alle loro rigidezze e non “si stira” né “si taglia” in pianta.
Si confronta il rapporto di drift con i limiti di norma (in genere valori dell’ordine di pochi per mille dell’altezza di piano).Per i solai in c.a. gettati in opera / laterocemento con soletta collaborante ciò è tipicamente vero se:Soletta continua in c.a. (≥ 4–5 cm, armata) ben connessa a travi/cordoli e setti;Assenza di grandi aperture nel solaio (come ordine di grandezza, fori totali ≲ 15–20% della superficie e non a tagliare il diaframma);Ancoraggi e cordoli perimetrali continui (catene, cordoli in c.a., staffe/passanti);Geometria compatta (niente ali sottili senza giunti) e luci ordinarie (6 m in questo caso);Piano unico o pochi dislivelli, senza giunti che interrompano la continuità di soletta.Con queste condizioni la rigidezza nel piano del solaio in c.a. è di molto superiore alla rigidezza laterale dei telai/setti ⇒ diaframma rigido è quindi la più appropriata.Viceversa la copertura in legno (tradizionale) non è rigidaI tetti in legno “classici” (capriate/puntoni + assito o perlinato + manto) non hanno di per sé un sistema di taglio nel piano (shear diaphragm) paragonabile a una soletta in c.a. in quanto mancano:un pannello continuo con rigidezza a taglio (OSB/compensato/XLam) con schema di chiodatura/collaggio certificato;travi di bordo e collegamenti a cordoli/setti dimensionati per le forze di diaframma;controventi nel piano (croci, cavi) che rendano il tetto indeformabile nel proprio piano.Quindi, salvo accorgimenti specifici, il tetto in legno va modellato come diaframma deformabile (o addirittura “a carichi tributari”), lasciando che siano i telai/setti a prendersi l’azione orizzontale, e usando i collegamenti per trasferire solo le spinte locali.Cosa si intende per “carichi tributari”I carichi tributari (tributary loads) sono la porzione di carico che “spetta” a ciascun elemento strutturale (trave, pilastro, fondazione) in base all’area o al tratto di solaio che converge su quell’elemento.Con diaframmi flessibili/semirigidi (es. tetti in legno non pannellati), i tagli orizzontali si stimano spesso per carichi tributari, perché l’impalcato non redistribuisce per rigidezza come un diaframma rigido.In pre-dimensionamento: è il modo standard per ricavare qqq sulle travi e NNN sui pilastri da un carico da solaio.Se serve come rendere “rigida” anche una copertura in legnoSi può considerarla diaframma rigido solo se si realizza uno dei seguenti sistemi, con dettagli di progetto:Pannellatura strutturale continua (OSB/compensato ≥ 12–15 mm) inchiodata secondo schema (passi, bordi, campi) + chords di bordo e collegamenti a cordoli/setti verificati allo sforzo di membrana;XLam di spessore idoneo, giunzioni certificate e ancoraggi al cordolo;Controventi nel piano (nastri/croci in acciaio) con collegamenti e ancoraggi calcolati.In assenza di questi dettagli costruttivi nei software che lo richiedono (Edilus) non spuntare “diaframma rigido” per il tetto in legno.Quando calcolare la rigidità di un tettoQuando vale la pena calcolare (o modellare) la rigidità in piano del tetto invece di dare per scontato “rigido” o “flessibile”:Si calcola la rigidità se:Tetto in legno o lamiera e si vuol far lavorare come diaframma (pannellatura OSB/XLam, lamiera collaborante): in questo caso servono passo chiodi/viti, forze nei chords e collettori.Pianta irregolare (a L/T, ali sottili, grandi rientranze) o aperture ampie nel tetto: la rigidezza del diaframma governa torsione e ripartizione dei tagli.Trasferimenti di taglio (“transfer diaphragms”): coperture che devono deviare/traghettare le azioni verso pochi setti/telai, attici, sbalzi, corpi scala.Stiffness mismatch tra sistemi verticali (setti molto rigidi + telai più cedevoli): il comportamento globale dipende da quanto il tetto distribuisce per rigidezza (rigido) o per tributari (flessibile).Campate o tetti estesi (L grande, b grande) o coperture leggere con connessioni deformabili: il contributo di pannelli/connessioni può diventare dominante.Verifiche vento importanti (zone ventose, grandi falde/pensiline leggere) o elementi non strutturali fragili ancorati alla copertura: gli spostamenti nel piano vanno stimati.Edifici esistenti in muratura (o misti) dove il tetto deve regimentare le spinte fuori piano delle pareti: la capacità del diaframma è spesso l’ago della bilancia.Progetti prestazionali (pushover, NLTH) o controllo P–Δ di piano: la corretta Δdiaframma evita errori sulla domanda di drift dei telai/setti.Si può evitare assumendo un modello semplificato se…Solaio/cordolo in c.a. continuo: in genere è infinitamente rigido → si puo assumere diaframma rigido senza calcoli dedicati.Tetto in legno non pannellato (solo assito/perlinato) e non si vuole usarlo come diaframma: modellalo flessibile e si portano le azioni ai sistemi verticali per carichi tributari.Edificio piccolo e regolare, sismicità bassa, luci ≤ 6 m e nessun trasferimento complesso: l’assunzione rigido (per c.a.) o flessibile (per tetto legno tradizionale) è di norma sufficiente.Cosa si ricava quando si calcola la rigiditàSpostamento nel piano Δ=Δpannello+Δconnessioni+Δcorde e rigidezza K=V/Δ.Chords: sforzi assiali e armature/sezioni necessarie.Collettori e ancoraggi: forze nelle cuciture, passo chiodi/viti, staffe e piastre.Classe del diaframma (rigido/semirigido/flessibile) confrontando Δdiaframma con il drift di piano (regola pratica: se Δdiaframma≲ 10% del drift, è “rigido”).
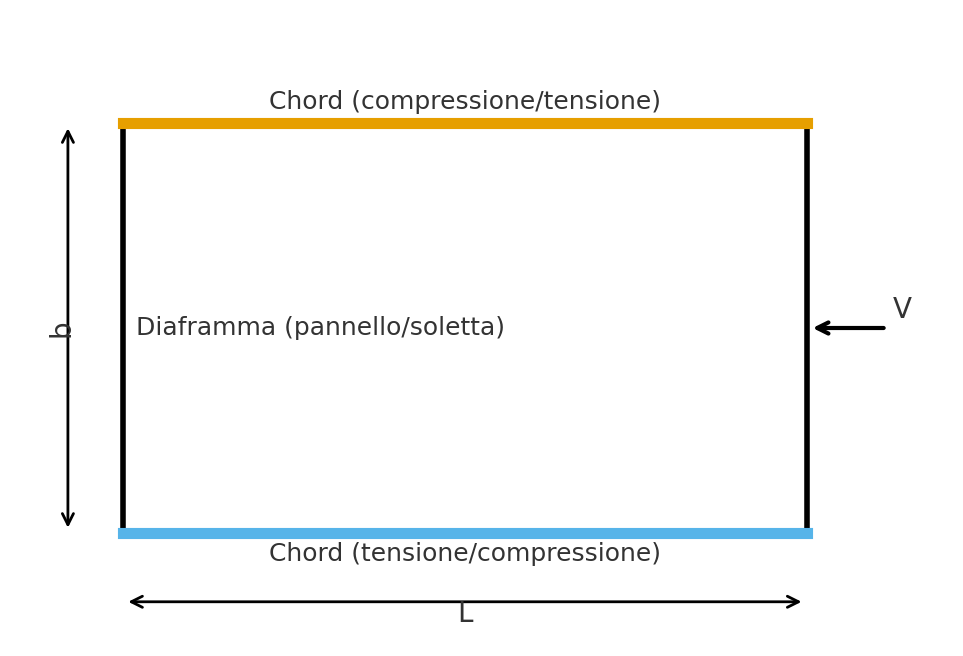
Come si calcola la rigidità di un diaframmaLa rigidità in piano di un diaframma (es. un tetto) si valuta come la capacità dell’impalcato di opporre deformazioni nel proprio piano sotto un taglio V applicato. Operativamente si scompone la freccia nel piano Δ in tre contributi:Δ=Δpannello+Δconnessioni+Δcordedove:Δpannello (taglio del pannello/soletta),Δconnessioni (scorrimento di chiodi/viti/connettori),Δcorde (allungamento/compressione dei longheroni di bordo, i “chords”).Modello matematico pratico per il calcolo della rigiditàDi seguito il modello pratico (valido per tetti/solai a pannellatura tipo OSB/compensato o lamiera grecata; per solette in c.a. la parte pannello domina e spesso rende l’impalcato “rigido”):Geometria e simboliL = lunghezza del diaframma (direzione della spinta) [m]b = “altezza” del diaframma (perpendicolare a L) [m]t = spessore pannello/soletta [m]V = taglio di piano applicato [N]G_eff = modulo di taglio effettivo del pannello (o soletta) [Pa]E_c, A_c = modulo elastico e area totale delle due corde (tensione+compressione) [Pa], [m²]K_{ser} = modulo di scorrimento (slip modulus) per singola connessione (chiodo/vite) [N/mm]s = passo delle connessioni lungo il bordo [m](si considerano due bordi lungo L che “portano” il taglio)1) Deformazione a taglio del pannelloΔpannello = V/ (b ⋅ t⋅ Geff ⋅ L)Deriva da γ=τ/G con τ=V/(b ⋅ t) e γ=Δ/L2) Scorrimento delle connessioni (bordo → travi/cordoli)Connessioni modellate come molle distribuite: la rigidezza per unità di bordo èk′ = Kser ⋅ 1000/s [N/m per ogni bordo]
(da N/mm a N/m moltiplicando per 1000). Con due bordi: ktot=2⋅k′.
|